Información importante
La Identidad de Euler
Partimos de la expresión de la exponencial en forma de serie:
Sustituímos x por z·i, usamos que ,
,
,
(a partir de aquí se va repitiendo el ciclo de resultados) y agrupamos las potencias pares de z por un lado y las impares por otro, obteniendo:
Sabiendo que las expresiones de sin x y cos x en forma de serie son:
llegamos a:
Sustituimos z por π (Pi):
Pasando -1 a la izquierda como +1 llegamos a la identidad buscada:
Serie de Fourier
La idea intrínseca de la sf nos
indica que cualquier función, generalmente periódica, se puede aproximar por
medio de funciones simples sinusoidales. De forma que cuanto más coincide una
onda simple con el dato observado, más peso tiene en la determinación de la
función original. (Con este procedimiento es posible representar funciones
deterministas o de índole aleatoria.) Con la sf se adquiere un cambio en el
dominio de la función; al pasar de la información contenida en una señal, al
dominio en el tiempo, para transitar al de la frecuencia y viceversa, de suerte
tal que se mejora el análisis de la señal (Carrillo, 2003). Así que las sf son
útiles en el estudio de funciones periódicas, aunque, desafortunadamente, no
aparecen con la misma frecuencia en la vida real como las no periódicas.
Definición y algoritmo de cálculo de la Serie de Fourier
Sea f(x) una función de una
variable real. Supongamos que dicha función es integrable en un determinado
intervalo de longitud T. Se define la serie de Fourier de f(x) como:
Por una parte, la sf es un método
más completo y más real que otras aproximaciones obtenidas por métodos como
mínimos cuadrados ordinarios (mco), promedios, entre otros; pues como
comentamos a lo largo del trabajo, ésta incorpora el comportamiento de las
observaciones, permitiéndonos observar tendencias y ciclos de los datos.
Empero, ese tema sobrepasa por mucho los alcances de este artículo, por lo que
se dejará para otro tema de investigación.
Por otra parte, la sf nos ayuda a
conocer el comportamiento de nuestros datos, por medio de una aproximación
trigonométrica, pero hay que mencionar que a una mayor cantidad de datos
observados mejor es la estimación realizada. En otras palabras, si el número de
datos tiende a infinito, entonces nuestro error tiende a cero, lo cual podría
ser un inconveniente a pesar de que el polinomio obtenido pasa por los datos
observados.
En adición, la aproximación
realizada por medio de Fourier es un método completamente determinístico,
ausente de perturbaciones aleatorias. Puesto que con el conjunto de datos
establecido, siempre obtendremos la misma reproducción a menos que
implementemos una variación al agregar o quitar datos de la muestra.
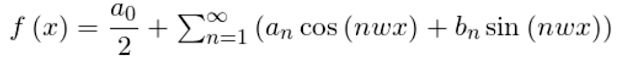


Comentarios
Publicar un comentario